Data Structure means different ways of storing data on your computer while algorithms are operations that we can perform on different data structures and the set of instructions for executing them. Without data structures, you can't use algorithms.
Data Structures are all about rendering data elements regarding some relationship or better organization and storage. Therefore, anything that can store data can be called as a data structure. It might be an integer, Boolean, or char value otherwise known as primitive data structures.
Complex Data Structures:
This set of data is used to store large and connected data. Some examples are: Trees including: binary, binary heaps etc., Linear which can be arrays or lists, Hash: distributed hash tree or tables and Graphs: directed, acyclic etc.
Based on the requirements and what type of operation should be executed, then the useful data structure must be chosen.
Let’s now take a look at the tree data structure, specifically at heaps as it makes up a few of the more well-known data structures.
First, the notion of 'tree' represents a hierarchical structure made of the root value and its children subtrees (with a parent node), represented as a set of linked nodes. A tree comprises 'nodes' which have a value associated with it and each of them are linked together by a line named 'edge'. These lines display the relationship between nodes. The first and top-level node is known as the 'parent' or 'root' and the nodes without 'children' are called 'leaf'. If nodes are linked together, then the previous node is referred as 'parent' and the nodes following it are called 'child' nodes. Even though there are various types of tree structures, today we are going to talk about heaps.
Feature #1: What are Heaps?
A heap is a complete binary tree that satisfies the heap property. For a binary tree every node can contain zero, one or two children and it has to be a complete tree. Every level of the tree is full, except potentially the last level. And on the last level, if it is not complete, meaning that every leaves parent doesn't have two children, so if there is any space at the bottom level, the existing leaves all have to be as far to the left as possible. Heaps have two requirements. So, the first requirement is that the heap must be a binary tree. The second one, is that it must satisfy the heap property and the latter will depend whether we are talking for a max heap or a min heap.
Max Heap: when it comes to max heap, every parent has a value greater than or equal to its children. On the contrary a min heap, every parent has to have a value less than or equal to its children. A binary tree must be a complete tree. When creating a heap, we add children at each level from left to right. So, if we would add a bunch of values into an empty heap then the first value would become the root, the second value would be the left child of the root, the third value would become the right child of the root and then we would come down to the next level and so forth.
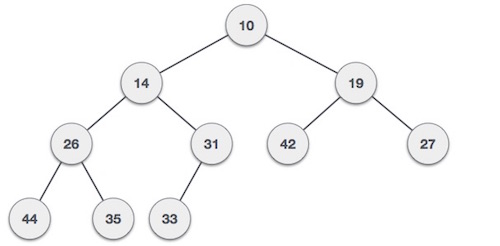Heap Structure
Heaps implemented as Arrays
Another important aspect of heaps is that they are implemented as arrays. When you have a complete binary tree then you have to back them up by arrays. That is how heaps are usually implemented. Now, because of the heap property, the maximum or minimum value will always be at the root of the tree and that's why heaps exist. In case of a max value in a max heap or min value in min heap, the value will always be at the root. Therefore, you will always have the max or min value in a constant time.
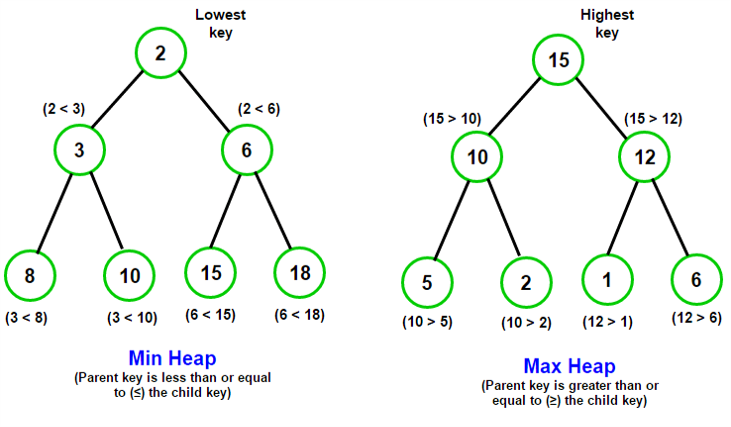Min vs. Max Heap
Heapify Process
When we insert a node value into the tree then it is basically added to the bottom level as before mentioned when you build a tree, you start at the top and then move to the next level, add nodes left-to-right and then to the next level left-to-right and so on. Fixing the tree according to heap requirements is a process called heapify.
Heapify is a process of converting the binary tree into a heap, this often has to be done after an insertion or deletion. A visual image of the heapify process is shown below.
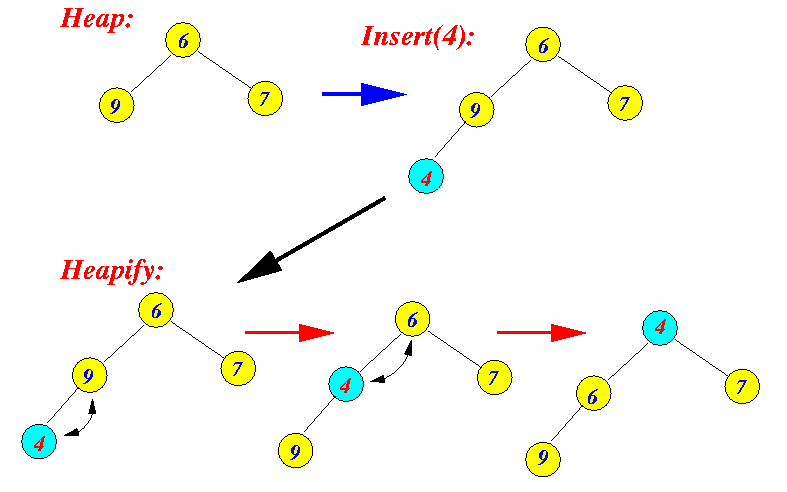Heapify Process
In conclusion, there is no required ordering between siblings, so when you have nodes at the same level they don't have to be in descending or ascending order. What is important in relation to heaps is the relative values between parents and children.
Service
