Datenstrukturen: Einführung in Heaps
Bei Datenstrukturen geht es darum, Datenelemente in Bezug auf eine Beziehung oder eine bessere Organisation und Speicherung zu rendern. Daher kann alles, was Daten speichern kann, als Datenstruktur aufgerufen werden. Dies kann ein ganzzahliger, boolescher oder char-Wert sein, der auch als primitive Datenstrukturen bezeichnet wird.
Komplexe Datenstrukturen:
Dieser Datensatz wird zum Speichern großer und verbundener Daten verwendet. Einige Beispiele sind: Bäume, einschließlich: binäre, binäre Heaps usw., lineare, die Arrays oder Listen sein können, Hash: verteilter Hash-Baum oder Tabellen und Diagramme: gerichtet, azyklisch usw.
Basierend auf den Anforderungen und der Art der Operation, die ausgeführt werden soll, muss die nützliche Datenstruktur ausgewählt werden.
Schauen wir uns nun die Baumdatenstruktur an, insbesondere die Haufen, da sie einige der bekannteren Datenstrukturen ausmacht.
Erstens stellt der Begriff "Baum" eine hierarchische Struktur dar, die aus dem Stammwert und seinen untergeordneten Teilbäumen (mit einem übergeordneten Knoten) besteht und als Satz verknüpfter Knoten dargestellt wird. Ein Baum besteht aus "Knoten", denen ein Wert zugeordnet ist, und jeder von ihnen ist durch eine Linie mit dem Namen "Kante" miteinander verbunden. Diese Linien zeigen die Beziehung zwischen Knoten an. Der Knoten der ersten und obersten Ebene wird als "Eltern" oder "Wurzel" bezeichnet, und die Knoten ohne "Kinder" werden als "Blatt" bezeichnet. Wenn Knoten miteinander verbunden sind, wird der vorherige Knoten als "übergeordneter Knoten" bezeichnet, und die darauf folgenden Knoten werden als "untergeordnete Knoten" bezeichnet. Obwohl es verschiedene Arten von Baumstrukturen gibt, werden wir heute über Haufen sprechen.
Feature # 1: Was sind Haufen?
Permalink to "Feature # 1: Was sind Haufen?"Ein Heap ist ein vollständiger Binärbaum, der die Heap-Eigenschaft erfüllt. Für einen Binärbaum kann jeder Knoten null, ein oder zwei untergeordnete Knoten enthalten und muss ein vollständiger Baum sein. Jede Ebene des Baums ist voll, mit Ausnahme der möglicherweise letzten Ebene. Und auf der letzten Ebene, wenn es nicht vollständig ist, was bedeutet, dass jeder Elternteil keine zwei Kinder hat. Wenn also auf der unteren Ebene Platz ist, müssen alle vorhandenen Blätter so weit wie möglich links liegen. Haufen haben zwei Anforderungen. Die erste Anforderung ist also, dass der Heap ein Binärbaum sein muss. Das zweite ist, dass es die Heap-Eigenschaft erfüllen muss und letztere davon abhängt, ob es sich um einen Max-Heap oder einen Min-Heap handelt.
Max Heap: Wenn es um Max Heap geht, hat jeder Elternteil einen Wert, der größer oder gleich seinen Kindern ist. Im Gegenteil, jeder Elternteil muss einen Wert haben, der kleiner oder gleich seinen Kindern ist. Ein Binärbaum muss ein vollständiger Baum sein. Beim Erstellen eines Heaps fügen wir auf jeder Ebene von links nach rechts untergeordnete Elemente hinzu. Wenn wir also eine Reihe von Werten zu einem leeren Heap hinzufügen würden, würde der erste Wert zur Wurzel werden, der zweite Wert wäre das linke Kind der Wurzel, der dritte Wert würde das rechte Kind der Wurzel und dann würden wir Komm runter zum nächsten Level und so weiter.
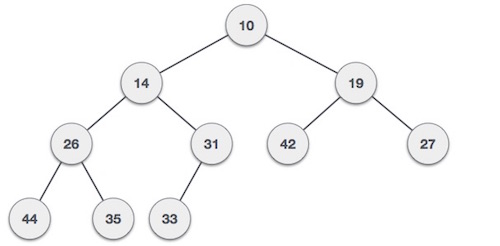
Als Arrays implementierte Heaps
Permalink to "Als Arrays implementierte Heaps"Ein weiterer wichtiger Aspekt von Heaps ist, dass sie als Arrays implementiert sind. Wenn Sie einen vollständigen Binärbaum haben, müssen Sie diese durch Arrays sichern. So werden Heaps normalerweise implementiert. Aufgrund der Heap-Eigenschaft befindet sich der Maximal- oder Minimalwert immer im Stammverzeichnis des Baums, weshalb Heaps vorhanden sind. Bei einem Max-Wert in einem Max-Heap oder einem Min-Wert in einem Min-Heap befindet sich der Wert immer an der Wurzel. Daher haben Sie immer den Maximal- oder Minimalwert in einer konstanten Zeit.
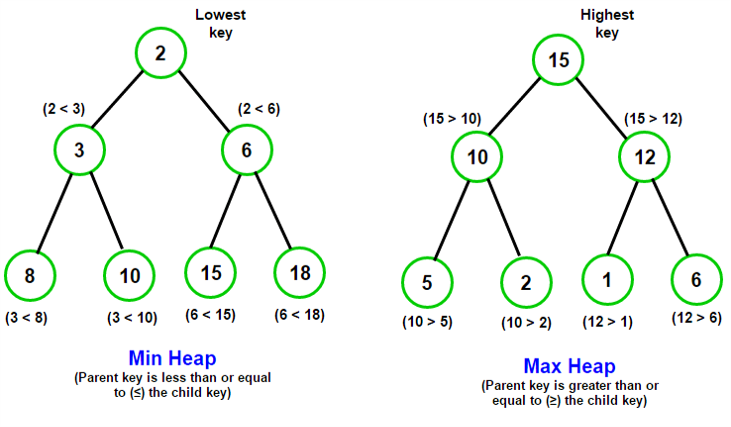 Min vs. Max Heap
Min vs. Max Heap
Heapify-Prozess
Permalink to "Heapify-Prozess"Wenn wir einen Knotenwert in den Baum einfügen, wird dieser im Grunde genommen der untersten Ebene hinzugefügt, wie zuvor erwähnt, wenn Sie einen Baum erstellen. Sie beginnen oben und wechseln dann zur nächsten Ebene, fügen Knoten von links nach rechts und dann zu hinzu die nächste Ebene von links nach rechts und so weiter. Das Fixieren des Baums gemäß den Heap-Anforderungen wird als Heapify bezeichnet.
Heapify ist ein Prozess zum Konvertieren des Binärbaums in einen Heap. Dies muss häufig nach dem Einfügen oder Löschen erfolgen. Ein visuelles Bild des Heapify-Prozesses ist unten dargestellt.
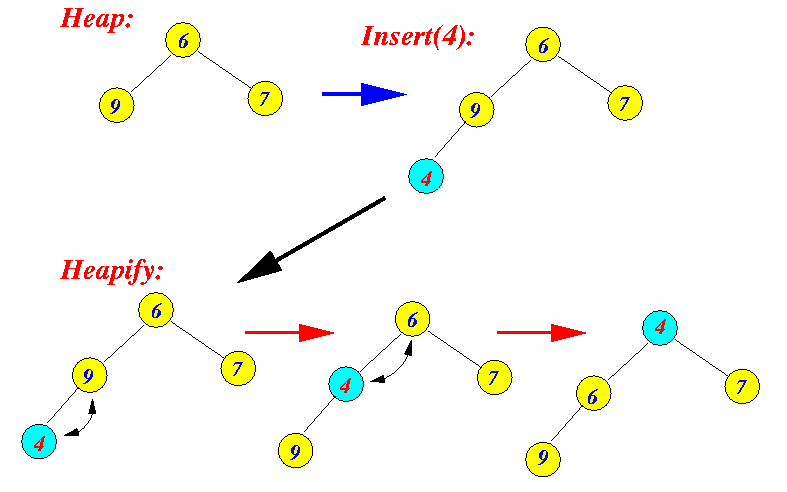 Heapify Process
Heapify Process
Zusammenfassend lässt sich sagen, dass keine Reihenfolge zwischen Geschwistern erforderlich ist. Wenn Sie also Knoten auf derselben Ebene haben, müssen diese nicht in absteigender oder aufsteigender Reihenfolge sein. Was in Bezug auf Haufen wichtig ist, sind die relativen Werte zwischen Eltern und Kindern.